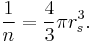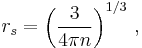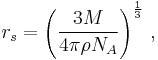Wigner–Seitz radius

The Wigner–Seitz radius 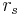$r_s$ , named after Eugene Wigner and Frederick Seitz, is a parameter used frequently in condensed matter physics to describe the density of a system. The formula for 3-D system is

$\frac{1}{n} = \frac{4}{3} \pi r_s^3.$

Solving for 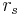$r_s$ we obtain

$r_s = \left(\frac{3}{4\pi n}\right)^{1/3}\,,$

where $n$ is the particle density of the valence electrons.

For a non-interacting system, the average separation between two particles will be 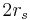$2 r_s$ . The radius can also be calculated as

$r_s= \left(\frac{3M}{4\pi \rho N_A}\right)^\frac{1}{3}\,,$

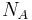where $M$ is molar mass, $\rho$ is mass density, and $N_A$ is the Avogadro number.

This parameter is normally reported in atomic units, i.e., in units of the Bohr radius.

Wigner–Seitz radius

See also